Steam Power Software - Web-Based analysis of Steam Power Plants, Cogeneration, and Binary Cycles

Ex Consider a steam power plant operating on the simple ideal Rankine cycle. The steam enters the turbine at 4 MPa and 400^oC and is condensed in the condenser at a pressure of 100 kPa. Determine (a) the thermal efficiency and (b) net output in kJ/kg of the cycle. (c) What-if scenario: How would the answer change if the condenser pressure is reduced to 10 kPa?

Steam power plant operating on the simple ideal Rankine cycle

Step-by-Step Solution (expand/hide)

Detailed analysis of cycles, executed by a fluid flowing through open devices, is carried out by the open cycle TESTapps located in the specific branch of the open steady TESTapps. Launch the open cycle TESTapp located at the page TEST. TESTapps. Systems. Open. Steady. Specific. PowerCycles. PC Model.

Let us set up the cycle as follows: Device-A (turbine): isentropic expansion from State-1 to State-2 ; Device-B (condenser): constant pressure heat rejection from State-2 and State-3; Device-C (pump): isentropic compression from State-3 to State-4; Device-D (boiler): constant pressure heat addition from State-4 to State-1 .

Evaluate the states as follows. Assume a mass flow rate of 1 kg/s as a basis. H2O is the default fluid. For each state enter the known properties, and press the Enter key.

State-1: Enter p1, T1, and mdot1 (assume 1 kg/s), and Calculate.

State-2: Enter p2, s2 ('=s1'), mdot2 ('=mdot1'), and Calculate.

State-3: Enter p3 ('=p2'), x3 (=0 for saturated liquid), mdot3 ('=mdot1'), and Calculate.

State-4: Enter p4 ('=p1'), s4 ('=s3'), mdot4 ('=mdot1'), and Calculate.

Verify the calculated states graphically on a T-s diagram (as shown below). Notice that state-4 is coincident with state-3 (can you explain why?).

Having evaluated the principle states, it is time for setting up the four devies. Switch to the device panel and analyze each device as follows.

Device-A (Turbine): Load state-1 as the i1-state and state-2 as the e1-state, enter Qdot=0, and Calculate. Wdot_ext is calculated as 758 kW.

Device-B (Condenser): Load state-2 as the i1-state and state-3 as the e1-state, enter Wdot_ext=0, and Calculate. Qdot is calculated as -2037 kW.

Device-C (Pump): Load state-3 as the i1-state and state-4 as the e1-state, enter Qdot=0, and Calculate. Wdot_ext is calculated as -4.07 kW.

Device-D (Boiler): Load state-4 as the i1-state and state-1 as the e1-state, enter Wdot_ext=0, and Calculate. Qdot is calculated as 2792 kW.

Now switch to the cycle panel to find the thermal efficiency and net output calculated as 27.0% and 754.1 kJ/kg. (because mdot was chosen as 1 kg/s, the magnitude of Wdot_net/mdot is same as that of Wdot_net).

For the parametric study, change p2 to 10 kPa, press the Enter key, and Super-Cal to update all calculations. The new answers are calculated in the cycle panel as 35.3% and 1065 kJ/kg (see below). The minimum temperature in the cycle, 45.8 deg-C, is still high enough for the condenser to be cooled by circulating water at ambient temperature.

The TEST-code, generated by the Super-Cal operation, are listed below. Note how closely the codes follow the solution procedure.

#
# TEST-code: The code describes the solution procedure in a nut shell and can recreate the visual solution.
# TESTapp Path: TEST>TESTapps>Systems>Open>SteadyState>Specific>PowerCycle>PC Model

States {
State-1: H2O;
Given: { p1= 4.0 MPa; T1= 400 deg-C; Vel1= 0.0 m/s; z1= 0.0 m; mdot1= 1 kg/s; }

State-2: H2O;
Given: { p2= 100 kPa; s2= "s1" kJ/kg.K; Vel2= 0.0 m/s; z2= 0.0 m; mdot2= "mdot1" kg/s; }

State-3: H2O;
Given: { p3= "p2" kPa; x3= 0 fraction; Vel3= 0.0 m/s; z3= 0.0 m; mdot3= "mdot1" kg/s; }

State-4: H2O;
Given: { p4= "p1" kPa; s4= "s3" kJ/kg.K; Vel4= 0.0 m/s; z4= 0.0 m; mdot4= "mdot1" kg/s; }
}

Analysis {
Device-A: i-State = State-1; e-State = State-2; Mixing:true;
Given: {Qdot= 0.0 kW; T_B= 25.0 deg-C; }

Device-B: i-State = State-2; e-State = State-3; Mixing:true;
Given: { Wdot_ext= 0.0 kW; T_B= 25.0 deg-C; }

Device-C: i-State = State-3; e-State = State-4; Mixing:true;
Given: {Qdot= 0.0 kW; T_B= 25.0 deg-C; }

Device-D: i-State = State-4; e-State = State-1; Mixing:true;
Given: { Wdot_ext= 0.0 kW; T_B= 25.0 deg-C; }
}

Ex In a steam power plant operating on a reheat Rankine cycle, steam enters the HP turbine at 15 MPa and 620^oC and is condensed in the condenser at a pressure of 15 kPa. If the moisture content in the turbine is not to exceed 10%, determine (a) the reheat pressure and (b) the thermal efficiency of the cycle. (c) What-if scenario: How would the answers change if the moisture content in the turbine was not to exceed 15%?
Solution Detailed analysis of cycles executed by a fluid, passing through open devices connected back to back in a loop, is carried out by the open cycle TESTapps located in the specific branch of the open steady TESTapps.

Step-by-Step Solution (expand/hide)

#
# TEST-code: The code describes the solution procedure in a nut shell and can recreate the visual solution.
# TESTapp Path: TEST>TESTapps>Systems>Open>SteadyState>Specific>PowerCycle>PC Model

   States {
      State-1: H2O;
      Given:       { p1= 0.015 MPa;   x1= 0.0 %;   Vel1= 0.0 m/s;
           z1= 0.0 m;   mdot1= 1.0 kg/s;   }

      State-2: H2O;
      Given:       { p2= 15.0 MPa;   s2= "s1" kJ/kg.K;
            Vel2= 0.0 m/s;   z2= 0.0 m;   }

      State-3: H2O;
      Given:       { p3= "p2" MPa;   T3= 620.0 deg-C;
            Vel3= 0.0 m/s;   z3= 0.0 m;   }

      State-4: H2O;
      Given:       { p4= "p5" MPa;   s4= "s3" kJ/kg.K;
            Vel4= 0.0 m/s;   z4= 0.0 m;   }

      State-5: H2O;
      Given:       { T5= "T3" deg-C;   s5= "s6" kJ/kg.K;
            Vel5= 0.0 m/s;   z5= 0.0 m;   }

      State-6: H2O;
      Given:       { p6= "p1" MPa;   x6= 90.0 %;   Vel6= 0.0 m/s;
            z6= 0.0 m;   }
}

Analysis {
Device-A: i-State = State-1; e-State = State-2; Mixing: true
Given: { Qdot= 0.0 kW; T_B= 25.0 deg-C; }

      Device-B: i-State = State-2, State-4;
            e-State = State-3, State-5; Mixing: false
      Given: { Wdot_ext= 0.0 kW;   T_B= 25.0 deg-C;   }

Device-C: i-State = State-3; e-State = State-4; Mixing: true
Given: { Qdot= 0.0 kW; T_B= 25.0 deg-C; }

Device-D: i-State = State-5; e-State = State-6; Mixing: true
Given: { Qdot= 0.0 kW; T_B= 25.0 deg-C; }

Device-E: i-State = State-6; e-State = State-1; Mixing: true
Given: { Wdot_ext= 0.0 kW; T_B= 25.0 deg-C; }
}

Launch the open cycle TESTapp located at the page TEST. TESTapps. Systems. Open. Steady. Specific. PowerCycles. PhaseChange.

Let us set up the cycle as follows: Device-A: isentropic pumping from State-1 to State-2 ; Device-B : constant pressure boiler with State-2 and State-4 as inlets and State-3 and State-5 as exits; Device-C : high pressure isentropic turbine from State-3 to State-4 ; Device-D : low pressure isentropic turbine from State-4 to State-5 ; Device-E : constant pressure heat rejection from State-4 to State-1 .

State-1: Enter mdot1 (assume 1 kg/s), p1 (15 kPa) and x1 (0%). Calculate .

State-2: Enter p2 (15 MPa), s2 ('=s1'), and Calculate.

State-3: Enter p3 ('=p2'), T3 (620C) and Calculate.

State-4: Enter p4 ('=p5'), s4 ('=s3'), and Calculate. Note that p5 is not yet known.

State-5: Enter T5 ('=T3'), s5 ('=s6') and Calculate . Note that s6 is not yet known.

State-6: Choose 'More...' from the state selector to add more states to the menu. Choose State-6. Enter p6 ('=p1'), x6 (90%) and Calculate.

Super-Cal to propagates s6 back to State-5 and then p5 back to State-4, thus completing evaluation of all states. It is always a good practice to draw a T-s or some other thermodynamic plot to visualize the calculated states before proceeding to other panels.

Fig. 9.2.1 State-4. Only after State-6 is Calculated, is State-4 updated by Super-Cal.

In the device panel, work on the five devices.

Device-A: Select State-1 and State-2 as the i1- and e1-States , enter Qdot=0, and Calculate. The pumping power is calculated as -15.17 kW.

Device-B: Select State-2 and State-4 as the i1- and e1-States , and State-3 and State-5 as the e1- and e2-States , Calculate. Click on the 'non-mixing' radio button. Enter Wdot_ext=0. The heat transfer is 3831 kW (note that we could have broken the boiler into two devices, steam generator and superheater) .

Device-C: Select State-3 and State-4 as the i1- and e1-States , enter Qdot=0, and Calculate. The work is calculated as Wdot_ext=360 kW.

Device-D: Select State-5 and State-6 as the i1- and e1-States , enter Qdot=0 kW and Calculate. The work is calculated as Wdot_ext=1349 kW.

On the Cycle panel, no further work is necessary. The thermal efficiency is calculated as eta_th=44.2% .

Use Super-Cal to produce detailed output and the TEST-code. Use Super-Iterate for further iteration if the solution is not complete.

This is one of the rare instances where the Super-Iterate button has been used. One could avoid that by working in modules. Working on State-1,3,4 and Device-d (a Super-Cal among them will completely evaluate State-1) first will reduce the need for iterations.

For the parametric study, change x6 to 85%, Calculate and Super-Cal to obtain the new efficiency as 43.24% (the efficiency increases with moisture content for cycles without superheat).

Fig. 9.2.2 Device panel (Device-B, the boiler). Notice that the Non-Mixing option must be turned on
for the non-mixing flow of a heat exchanger.

Ex A regenerative vapor power cycle has two turbine stages with steam entering the first turbine stage at 8 MPa and 550^oC and expanding to 700 kPa, where some of the steam is extracted and diverted to the open feed water heater operating at 700 kPa. The remaining steam expands through the second turbine stage to condenser pressure of 7 kPa. Saturated liquid exits the open feedwater heater at 700 kPa. Each turbine stage has an isentropic efficiency of 88% and each pump has an isentropic efficiency of 80%. Determine (a) the thermal efficiency of the cycle, (b) the net power developed, and (c) the fraction of flow exracted where bleeding occurs. (c) What-if scenario: How would the answers change if the bleeding occurs at 500 kPa?

Step-by-Step Solution (expand/hide)

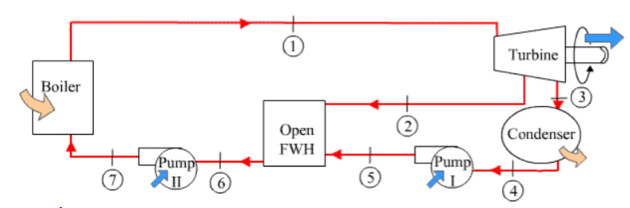
Launch the open cycle TESTapp located at the page TEST. TESTapps. Systems. Open. Steady. Specific. PowerCycles. PC Model.

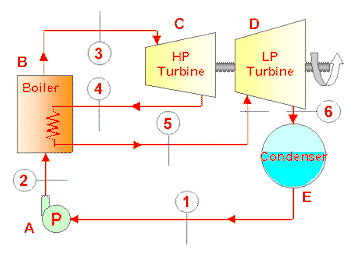
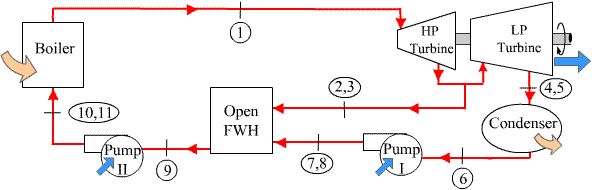
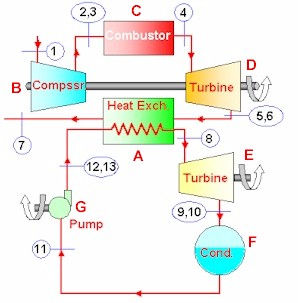
Let us set up the cycle as follows: Device-A (turbines): Instead of treating the two turbines separately, let us analyze them as a composite device with two exits, State-3 and State 5, and one inlet, State-1. Note that State-2 and 4 are isentropic states, which are necessary to evaluate the actual exit states. Device-B (condenser): Constant pressure heat rejection from State-5 to State-6. Device-C (pump-I): Compression from State-6 to State-8 (with State-7 being the isentropic state). Device-D (FWH): Constant pressure mixing between State-3 and State-8, producing State-9. Device-E (pump-II): Compression from State-9 to State-11; (with State-10 being the isentropic state). Device-F (boiler): constant pressure heat addition from State-11 to State-1.

Let us assume a mass flow rate of 1 kg/s through the boiler and leave mdot3 (the rate of bleeding) unknown, expressing all other mass flow rates in terms of mdot1 and mdot3. Evaluate the states as follows.

State-1: Enter p1, T1, and mdot1 (assume 1 kg/s), and Calculate.

State-2: Enter p2, s2 ('=s1'), mdot2 ('=mdot1'), and Calculate.

State-3: Enter p3 ('=p2'), h3 ('=h1+(h2-h1)*0.88'), and Calculate (mdot3 is unkown at this point).

State-4: Enter p4 ('=p1'), s4 ('=s3') and Calculate (mdot4 is never used and so can be left unknown).

State-5: Enter p5 ('=p4'), h5 ('=h3+(h4-h3)*0.88'), mdot5 ('=mdot1-mdot3'), and Calculate (mdot5 is unkown at this point).

State-6: Enter p6 ('=p4'), x6 ('=0', saturated liquid), mdot6 ('=mdot1-mdot3'), and Calculate (mdot6 is unkown at this point).

State-7: Enter p7 ('=p2'), s7 ('=s6') and Calculate (mdot7 is never used and so can be left unknown).

State-8: Enter p8 ('=p2'), h5 ('=h6-(h6-h7)/0.8'), mdot8 ('=mdot1-mdot3'), and Calculate (mdot8 is unkown at this point).

State-9: Enter p9 ('=p2'), x9 ('=0', saturated liquid), mdot9 ('=mdot1'), and Calculate.

State-10: Enter p10 ('=p1'), s10 ('=s9') and Calculate (mdot10 is never used and so can be left unknown).

State-11: Enter p11 ('=p1'), h11 ('=h9-(h9-h10)/0.8'), mdot11 ('=mdot1'), and Calculate.

Having evaluated the principle states as best as possible, it is time for setting up the devies. Switch to the device panel and analyze each device as follows.

Device-A (Turbine): Load state-1 as the i1-state, and state-3 and 5 as the e1 and e2 states respectively. Enter Qdot=0, and Calculate. Wdot_ext cannot be calculated at this time as mdot3 is still an unknown.

Device-B (Condenser): Load state-5 as the i1-state and state-6 as the e1-state, enter Wdot_ext=0, and Calculate. Qdot is unknown at this point.

Device-C (Pump): Load state-6 as the i1-state and state-9 as the e1-state, enter Qdot=0, and Calculate. Wdot_ext is is unknown at this point.

Device-D (Heater): Load state-3 and 8 as the i1 and i2 states and state-9 as the e1-state. Enter Qdot=0 and Wdot_ext=0, and Calculate. The energy equation produces mdot3 and posts it back to state-3 as shown below. The fraction of steam that is extracted at state-3 is, therefore, 0.1924.

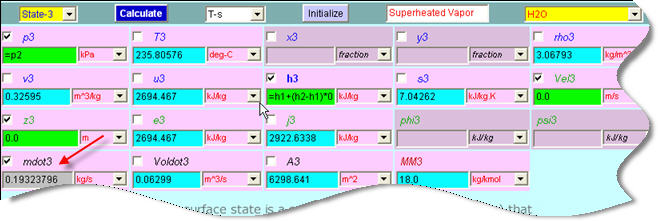
At this point we can do a Super-Cal to update all calculations. However, a few more devices remain to be analyzed.

Device-E (Pump-II): Load state-9 as the i1-state and state-11 as the e1-state, enter Qdot=0, and Calculate. Wdot_ext is calculated as -10.11 kW.

Device-F (Boiler): Load state-11 as the i1-state and state-1 as the e1-state. Enter Wdot_ext=0, and Calculate Qdot=2814 kW.

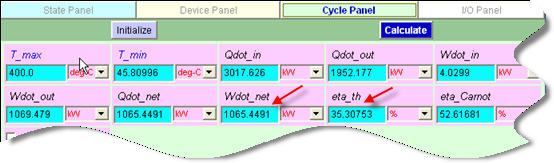
Super-Cal one more time to update the cycle panel. The thermal efficiency and net output are calculated as 39.44% and 1109.6 kW respectively.

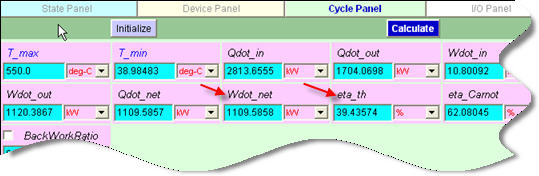
For the what-if scenario, change p2 to 500 kPa, press the Enter key, and Super-Cal. The new answers are found to be mdot3=0.1764 kg/s, eta_th=39.35%, and Wdot_net= 1129.6 kW.

The TEST-Codes for the problem are reproduced below, which can be used to instanly regeneratre the solution (simply paste the TEST-code into the I/O panel, click the Load button and then Super-Cal).

#
# TEST-code: The code describes the solution procedure in a nut shell and can recreate the visual solution.
# TESTapp Path: TEST>TESTapps>Systems>Open>SteadyState>Specific>PowerCycle>PC Model

States {
State-1: H2O;
Given: { p1= 8.0 MPa; T1= 550.0 deg-C; Vel1= 0.0 m/s; z1= 0.0 m; mdot1= 1.0 kg/s; }

State-2: H2O;
Given: { p2= 700.0 kPa; s2= "s1" kJ/kg.K; Vel2= 0.0 m/s; z2= 0.0 m; }

State-3: H2O;
Given: { p3= "p2" kPa; h3= "h1+(h2-h1)*0.88" kJ/kg; Vel3= 0.0 m/s; z3= 0.0 m; }

State-4: H2O;
Given: { p4= 7.0 kPa; s4= "s3" kJ/kg.K; Vel4= 0.0 m/s; z4= 0.0 m; }

State-5: H2O;
Given: { p5= "p4" kPa; h5= "h3+(h4-h3)*0.88" kJ/kg; Vel5= 0.0 m/s; z5= 0.0 m; mdot5= "mdot1-mdot3" kg/s; }

State-6: H2O;
Given: { p6= "p4" kPa; x6= 0.0 fraction; Vel6= 0.0 m/s; z6= 0.0 m; mdot6= "mdot1-mdot3" kg/s; }

State-7: H2O;
Given: { p7= "p2" kPa; s7= "s6" kJ/kg.K; Vel7= 0.0 m/s; z7= 0.0 m; }

State-8: H2O;
Given: { p8= "p2" kPa; h8= "h6-(h6-h7)/0.8" kJ/kg; Vel8= 0.0 m/s; z8= 0.0 m; mdot8= "mdot1-mdot3" kg/s; }

State-9: H2O;
Given: { p9= "p2" kPa; x9= 0.0 fraction; Vel9= 0.0 m/s; z9= 0.0 m; mdot9= "mdot1" kg/s; }

State-10: H2O;
Given: { p10= "p1" kPa; s10= "s9" kJ/kg.K; Vel10= 0.0 m/s; z10= 0.0 m; }

State-11: H2O;
Given: { p11= "p1" kPa; h11= "h9-(h9-h10)/0.8" kJ/kg; Vel11= 0.0 m/s; z11= 0.0 m; mdot11= "mdot1" kg/s; }
}

Analysis {
Device-A: i-State = State-1; e-State = State-3, State-5; Mixing: true;
Given: { Qdot= 0.0 kW; T_B= 25.0 deg-C; }

Device-B: i-State = State-5; e-State = State-6; Mixing: true;
Given: { Wdot_ext= 0.0 kW; T_B= 25.0 deg-C; }

Device-C: i-State = State-6; e-State = State-8; Mixing: true;
Given: { Qdot= 0.0 kW; T_B= 25.0 deg-C; }

Device-D: i-State = State-3, State-8; e-State = State-9; Mixing: true;
Given: { Qdot= 0.0 kW; Wdot_ext= 0.0 kW; T_B= 25.0 deg-C; }

Device-E: i-State = State-9; e-State = State-11; Mixing: true;
Given: { Qdot= 0.0 kW; T_B= 25.0 deg-C; }

Device-F: i-State = State-11; e-State = State-1; Mixing: true;
Given: { Wdot_ext= 0.0 kW; T_B= 25.0 deg-C; }
}